Imagine you purchase Apple stock. By definition, you and the seller are on opposites sides of a binary trade – if Apple zooms up, you will have made money and the seller will presumably regret selling, and vice versa. Apple is most likely going to move one way or the other, so there’s going to be a winner and a loser.
Do structured notes present a similar binary outcome between buyer and seller? If the investing purchaser makes money, does the issuing bank lose money? And vice versa? The answer is a resounding no!
Why are We Interested?
Purchasers of structured notes sometimes believe the issuer automatically wins when they lose, which would place a bank in conflict with their clients. The short answer is that this is not the case. The outcome is not a zero-sum game and ultimately both the investor and bank can win. It is in an issuer’s best interest for the client to win in the long run as this would lead to an increase in both business and revenue – so yes, trading desks (mostly) root for the client. In this post, we will discuss the makeup of a structured note and how the trader at the issuing bank treats the product very differently than the client, resulting in a potential win-win situation.
Let’s first understand how each party is looking to benefit from a structured note:
From the investor’s perspective, as long as the bank is in business at maturity (i.e., the investor owns a note/credit), the investor’s payoff is easy to calculate based on the terms of the prospectus.
From the bank’s perspective, the note breaks down into three general components:
- Fees – some portion of the investment accrue directly to the bank as fee revenue for the departments that structured and distributed the note
- Credit Component – the bulk of the investment is made available to the bank’s treasury department; the bank is then generally free to use that money for any investment purpose it sees fit. Conceptually, a structured note is no different than a bond – a typically inexpensive way for the bank to access capital for a defined period of time. The treasury department of the bank is responsible for setting internal rates for borrowing and lending. How competitive a bank is on the credit component of a note is purely a function of whether the bank needs or wants funding – e.g., is there a balance sheet gap that needs to be filled, or is there a good expansion opportunity the bank is eyeing.
Note the Treasury departments “rate” that it pays the structured note is separate and distinct from how the street views the credit of the bank and therefore the fair market value of said credit. Therefore, there can be a disconnect in the rate provided by the bank and a presumed “fair-market” value of the credit component of a note. This becomes important when considering the more interest Treasury pays the structured note, the more the trading desk has to spend resulting in better characteristics (e.g., higher cap, more protection) for the note.
- Derivative Component – the remainder of the investment is priced by the derivatives trading desk in creating the derivatives strategy placed in the note (FYI – my former role).
Prior to the note being sold, the trading desk plays a critical role in creating interesting payoffs that will (a) sell in the market and (b) make money for the bank. As mentioned previously, the trading desk utilizes the interest rate from Treasury to design the payoff – the higher the rate, the more generous the trading desk can be to the investor in terms of payoff characteristics.
Once the note is sold, the desk is primarily tasked with taking the opposite position of the customer (e.g., if the note calls for delivering the upside of the S&P 500, the trading desk is responsible for delivering that upside and thus is short the position). Note, the trader typically calculates the “fair theoretical value” of the contract and adds a profit spread before taking the opposite position.
Now, what is the “fair theoretical value” of the contract? The theoretical value is derived by the trader based on market inputs such as volatility of the underlying security, interest rates, and dividend rates. As we mentioned, the trader adds a spread to this theoretical fair value - e.g., if the option fair value is $100, the trader may buy it at $99 and show $1 of theoretical profit. The spread will be based on how easy or hard it is to hedge the risks of taking on the position and how competitive the market is on that specific trade (e.g., spreads will get wider or narrower depending on competition - whether the desk feels the customer is shopping around for the best pricing or not).
If a trader was able to perfectly offset or “hedge” the trade, the profit would be locked in and the trader would be able to ignore the note until it expires. In other words, regardless of how the structured note performs, the bank would make the theoretical $1 from the example above but no more. Client results (gain or loss) would have no positive or detrimental impact, making it certainly possible that both bank and client come out ahead.
However, with structured notes, traders typically cannot automatically “lock in” a profit. These option positions are often customized for a particular structured note and are thus not liquid – going back to the example above, if the trader puts on the position at $99, there is no way for him to instantly sell that position for $100 and lock in the gain. Thus, despite the trader adding a spread, it is by no means ‘locked in”, meaning that the trader still must actively manage the trade in order to capture the theoretical profit made through adding the spread.
Because of that exposure, the desk is secondarily tasked with eliminating (“hedging”) the risk they have on their side of the bet. For instance, if the desk is short S&P 500 exposure to one customer they can be long S&P 500 exposure to another customer, thus removing any risk to market movement (“Delta” risk). (As mentioned above, given the customized nature of many structured notes, simply matching inverse exposures between customers is often not possible.)
A derivative position results in a number of risks and alternative methods of hedging said risks. Portfolio management gets even more complicated. And this is what makes derivative trading so complex, dynamic, and interesting – there are many choices (options!) of how to hedge. Let’s review a simple example by analyzing one element of a trade to drive home the point of the differentiated approaches between the end investor and professional trader.
Technical Analysis
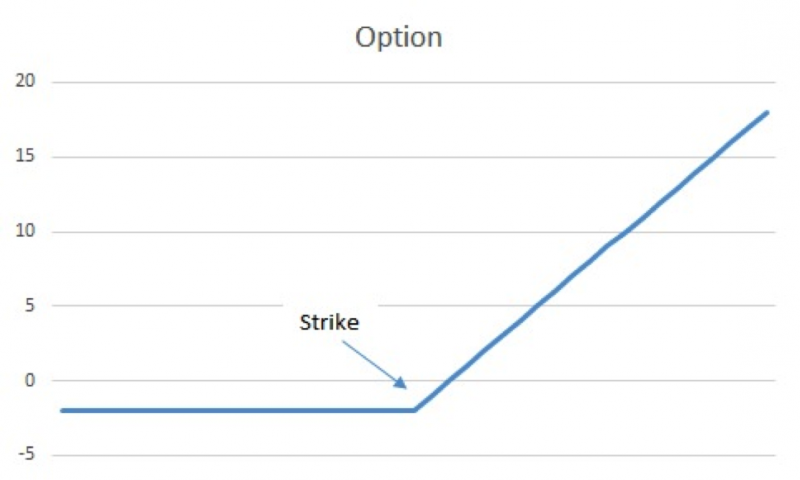
Let’s say we have a hypothetical stock, XYZ, and ignore dividends and interest rates for the moment. This hypothetical stock is trading at $100. There is an option on XYZ that allows for the purchase of XYZ at $100 that currently costs $2 (in option parlance a call option with a $100 strike which is At-The-Money (ATM)). Each option consists of 100 shares. If an investor believes XYZ will increase they may buy this option. It is certainly cheaper than buying the stock and thus limits the downside involved as the investor can only lose $2 as compared to $100 if XYZ goes to $0. If XYZ increases to $110, the investor makes $8. In conclusion, most investors view the purchase or sale of an option or a structured note as a way to take a position on the direction of the security.
Investor P&L:
Now let’s look at the perspective of the trading desk buying the same option as the investor. Typically, rather than focusing on whether XYZ will move up or down, the professional trader will treat this position by focusing on the way the security will move – the volatility (interest rate, dividends and other inputs also matter but volatility is the name of the game). So when this trader looks at the $2 option, they are not trying to analyze whether to be bullish or bearish on XYZ but rather how volatile XYZ will be during the remaining term of the option (note, this is a little simplistic as they might also care about perceived volatility – for example, is there an event on the horizon which will result in implied volatility increasing). This trader will look to “delta hedge” the option position in order to create a neutral view on the direction of the security, significantly adjusting the P&L of the position as outlined in the graph below.
How does he accomplish this hedge? Let’s assume there is a 50% chance XYZ will increase above $100 and a 50% chance XYZ will decrease from it (ignoring dividends and interest rates and assuming no upcoming major events for XYZ). The call option only makes money if XYZ increases, and as we mentioned earlier the trader wants to neutralize this outcome and become market neutral. So the trader “delta hedges” by selling short 50% of his theoretical long position. Now remember, an option consists of 100 shares. What the trader does is sell 50 shares of XYZ short at $100. I illustrate graphically the P&L of the various positions here:
Trading desk perspective:
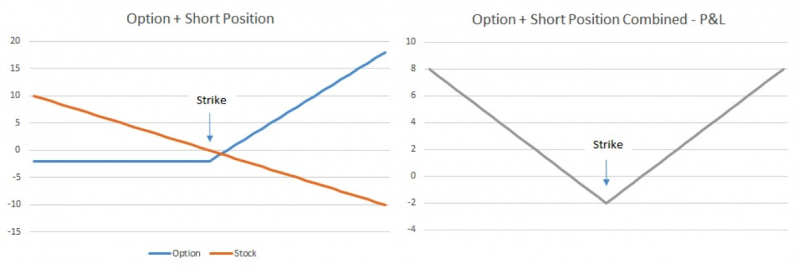
If XYZ increases to $110, the trader generates $800 in profit from the option but loses $500 on the stock position for a net positive of $300 (as compared to $800 for the option investor). If XYZ decreases to $90, the trader generates a $200 loss from the cost of the option but gains $500 on the stock position for a net positive of $300 (as compared to a $200 loss for the option investor). The trader makes money in either direction and the amount of gain is equal! The trader does not care which way the market goes, as long as it goes somewhere.
Now this is not a static one time hedge. The market is continuously adjusting, resulting in the “delta” constantly changing. Therefore hedging is constantly necessitated in order to remain neutral from a directional standpoint.
Let’s say XYZ moved from $100 to $95. At $100, we had decided there was a 50/50 chance the stock would move up or down but at $95, the odds must change. Let’s allocate a 60% chance that the stock remains below 100 and 40% above 100. Well that would necessitate an adjustment to the hedge. Instead of being short 500 shares, the trader would adjust by purchasing 100 shares to become net short 400 shares. If XYZ moves back to $100 then the trader would sell back out the 100 shares to have a short stock position of 500 shares. In other words, the trader is always adjusting the position resulting in multiple incremental gains. As long as the stock moves around enough – i.e., is volatile enough - a trader will make money on the option regardless of where the stock ultimately ends up. (A more advanced exercise can be to envision how to treat a short option position – perhaps a post for another time.)
The Takeaway
Investors and traders have different ultimate exposures to a derivatives trade. Structured notes, for example, allow the investor to construct a specified view of the market for the investor, who will buy and hold the strategy. The trading desk will hedge the derivative positions by offsetting with other derivatives or by delta hedging. The end result is that structured note trades are more complex than traditional I win/ you lose bets; there are structured scenarios in which both parties, one party, or neither party may win. In addition to any potential profit on the derivatives component, the bank is obtaining access to inexpensive cash when they issue a structured note, giving them yet other benefits to issuing a structured note and creating scenarios in which both the customer and bank can win. In conclusion, structured notes are not zero-sum games due to the participants (bank and client) treating their exposures very differently - the bank does not necessarily win when the investor loses and vice versa.
Joe Halpern is the CEO of Exceed Investments, an investment company focused on developing next-generation structured investments.

